实验3–图像滤波处理
图像滤波处理
3-1实现图像的高斯滤波处理
实验要求:
1)通过调整高斯函数的标准差(sigma)来控制平滑程度;
给定函数:void Gaussian(const MyImage &input, MyImage &output, double sigma);
2)滤波窗口大小取为[6sigma-1]/2*2+1,[.]表示取整;
3)利用二维高斯函数的行列可分离性进行加速;
- 先对每行进行一维高斯滤波,再对结果的每列进行同样的一维高斯滤波;
- 空间滤波=图像卷积;
- 高斯滤波=以高斯函数为卷积核的图像卷积。
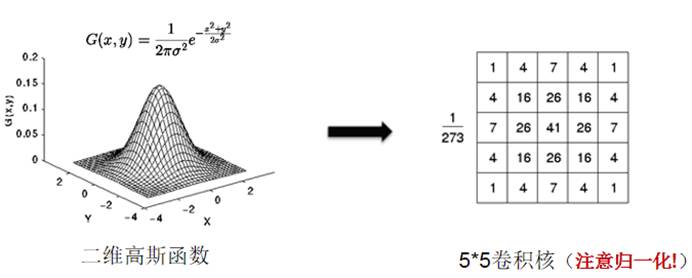
预期效果

二维高斯滤波
关于第二步滤波窗口的公式[6sigma-1]/2*2+1,为什么要先乘2再除2。
因为在很多C++中,整型数除2得到的结果仍为整型,再乘以2,加1,能使窗口边长为奇数个单位,但在python中,整数除法运算会自动转化为浮点数 ,以上操作无效,还需要额外取整。至于为什么要使边长为奇数(如3x3,5x5),原因就在于要以被处理像素点为中心,使像素取值能相对均匀。
先按照函数,实现一个行列不分离的高斯滤波器。
根据公式[6sigma-1]/2*2+1,可通过kernelSize= int(int(6*sigma-1)//2)*2+1得滤波窗口大小,//表示整除。然后构建Gaussian Kernel。
1 | Kernel=np.zeros((kernelSize,kernelSize),dtype=np.float) |
获得kernel后就可以对图像进行平滑操作filtering了。
1 | #改变参数 |
上面是两种平滑方式,其中filter2并不能实现给定函数Gaussian(const MyImage &input, MyImage &output, double sigma),即传入的图片并不能得到更改。函数内调用cv2.imshow()时可以正常显示,但是在主函数中,imgDst为纯黑。
1 | imgDst=np.zeros(list(imgSrc.shape),dtype='uint8') |
通过copy方法或者直接赋值是无法改变output的值的,其本质是使两个变量指向同一个地址。这是程序的参数传递性质决定的。保持函数filter2不变,可以通过return temp,然后在主函数中写img=Guassian(imgSrc,anyImg,sigma)实现图片的改变。
一个Kernel算法,两个filter算法(当然filter1相对来说更好,达到了预期效果)。二者呈现不同效果的主要原因还是在于python处理矩阵时的方式(或者说人编写程序的方式)。由于本人对其缺乏了解,尝试和改变了很多次,脑袋还是有些晕乎。两个filter交换一些写法,会出现各种行列匹配错误的问题。折腾了一个下午和晚上,属实费劲,真菜啊我。
一维高斯滤波
二维高斯分布函数:
$$G(x,y)=\frac{1}{2\pi\sigma^2}e^{-\frac{x^2+y^2}{2\sigma^2}}$$
二维高斯函数的行列可分离性的公式推导;
$$ \begin{equation}\begin{split}G(x,y)&=\frac{1}{2\pi\sigma^2}e^{-\frac{x^2+y^2}{2\sigma^2}}\&=\frac{1}{2\pi\sigma^2}e^{-\frac{x^2}{2\sigma^2}-\frac{y^2}{2\sigma^2}}\&=\frac{1}{2\pi\sigma^2}e^{-\frac{x^2}{2\sigma^2}}*\frac{1}{2\pi\sigma^2}e^{-\frac{y^2}{2\sigma^2}}\&=G(x)*G(y)\end{split}\end{equation} $$
高斯核行列分离
Kernel=np.zeros([kernelSize],dtype=np.float)
1 | # 高斯核行列分离转置 |
高斯核行列分离和两种滤波方式
1 | def SeperateGaussian(imgSrc,imgDst, sigma=1.2): |
对于两种滤波方式,显然前一种实现了效果,更新像素时的坐标处理也相对复杂,多一些细节的处理,对x轴和y轴的处理不能通过简单的复制粘贴来实现,而后者可以。num(Kernel*img[:,:,:],axis=0或1)中axis的加入也考察了对python的了解。axis=0表示对行(上下)进行操作计算,axis=1(左右)表示对列进行操作计算。
两种算法的性能对比
未采用行列分离的高斯滤波算法的时间复杂度为$O(N^2)$,分离后,时间复杂度降至$O(N)$。
当sigma=1.2时,
Gaussian()运行用时9.1567s,
SeperateGaussian()运行用时0.1357s;
opencv的函数cv2.GaussianBlur()运行时间仅为0.0062s;
显然opencv的方法也是使用了行列分离方式,不过其在细节处理上更优秀。
查阅资料可知,opencv实现的高斯滤波方法为cv2.GaussianBlur(src, ksize, sigmaX[, dst[, sigmaY[, borderType]]]) → dst,对传入的sigmaX,sigmaY分别产生两个一维卷积核,然后分别再行和列上做卷积,其中sigmaX和sigmaY如果没有传入参数,则由ksize计算得到。
以上运行时间同样与机器性能有关,不过经过多次测试,在本人机器上的运行时间相对稳定,可以体现不同实现方法在效率上的差距。
对不同sigma值的测试
原理
采用行列分离高斯滤波处理方法,测试不同sigma值(标准差)对图片的影响。
公式[6sigma-1]/2*2+1决定了滤波窗口(核)的大小,sigma值越大,窗口越大,图像也越平滑模糊。
高斯核的宽度与标准差σ的比值为6倍,为什么?
因为钟型曲线(高斯函数图像)在区间$(μ−σ,μ+σ)$范围内的面积占曲线下总面积的$68%$,$(μ−2σ,μ+2σ)$范围占$95%$,$(μ−3σ,μ+3σ)$范围占$99.7%$,一般$3σ$外的数值已接近于0,可忽略,半径为$3σ$即窗口大小为$6σ×6σ$即可,通常取最近的奇数。
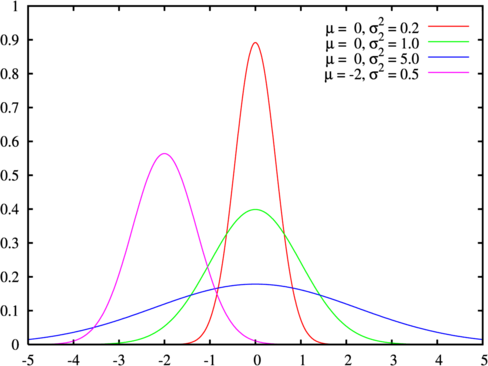
测试




参考资料
3-2实现图像的联合双边滤波处理
实验要求:
给定函数:function im = jbf(D,C,w, sigma_f, sigma_g)
其中:D为输入图像;C为引导图像;W为滤波窗口大小;
sigma_f 为spatial kernel标准差;
sigma_g为range kernel 标准差;
给定公式:
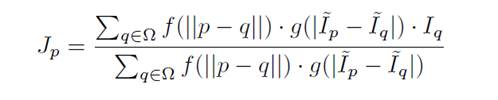
其中:p是q的邻域$Ω$中的一个像素。 f和g是空间和距离内核,通常以高斯的形式表示,$I$是输入图像。
- f 是空间滤波器内核,定义为:
exp([-d_f^2]/[2*sigma_f^2])
其中:d_f 为输入图像$I$的像素位置差,sigma_f为空间滤波核函数的标准差
- g是距离滤波器内核,定义为:
exp([-d_g^2]/[2*sigma_g^2])
其中:d_g为引导图像$I$ 的像素灰度值差,sigma_g为滤波核函数的标准差
输入图像*$I$*下采样(1/2)得到LR低分辨率图像,再由LR图像上采样2倍得到引导图像。
注:图像缩放采用双线性插值。
预期效果

JBF算法说明
高斯滤波处理图像时,不能很好的保持边缘。**双边滤波(Bilateral Filtering)**在这一点上有改善。双边滤波采用了两个高斯滤波的结合。一个负责计算空间邻近度的权值,也就是常用的高斯滤波器原理。而另一个负责计算像素值相似度的权值。双边滤波是去除图像中的噪声,同时保持细节和边缘清晰度的好方法,可用于电影修复、监控视频修复。
**联合双边滤波(Joint Bilateral Filtering,JBF)**是双边滤波的扩展,它接受两张图像的输入,其中一张是另一张图片的无闪光灯版本。第二张图像是用闪光灯拍摄的。这两个滤波器之间的唯一区别是,联合双边滤波器使用闪光灯图像的强度差异(difference in intensities),而不是正常的无闪光灯图像的强度差异。
摄影的目标是再现照片拍摄环境的丰富性。当环境中光线不足时,照片就会显得与环境不一样,而且很难看到图像的细节,因为它们被弄得很暗。闪光灯摄影解决了这个问题,它为环境中的附近物体增加了人工光线,这样相机就可以使用较短的曝光时间和较小的光圈宽度来捕捉足够的光线,产生闪光灯图像。这些图像的光照度更高,其清晰度也得到了提高,并消除了噪音。然而,闪光灯照片有一些缺点,如相机附近物体的亮度不相称,以及人们的红眼。联合双边滤波器利用无闪光灯和闪光灯图像的优点,产生一个清晰的无噪声的无闪光灯图像。$gr(Fp-Fp’)$占去了噪声,因为在闪光灯图像中没有噪声,乘以无闪光灯图像邻居的强度后,无闪光灯图像被重新创建,细节更多,噪声更少。
联合双边滤波器有很多应用,因为它是一个非常有效的滤波器。一个例子是去除图像中的雾气–该滤波器将去除图像中的大部分雾气,这样就更容易看到周围的环境。这样做的原因是闪光灯下的图像透过雾气有更高的可见度。另一个例子是医疗成像中的相机,它可以用来锐化图像的质量,以便更清楚地看到器官或内部细胞结构,从而得出准确的诊断。这是因为过滤器在使用有效的参数时,可以去除图像中的噪音,并使更精细的细节更加清晰。最后一个例子是在可见光或红外线过滤中。
以上说明来自某篇[报告](FaiZaman/Joint-Bilateral-Filter: An implementation and description of the joint bilateral filter in Python 3. (github.com)),用于学习JBF的理论知识和补充文章内容。
此外,实验说明中关于sigma_f和sigma_g的说明没有太理解,找了知乎上的一篇文章用于了解。
对于参数的选取,进行如下讨论:
首先,两个 sigma 值为 kernel 的方差,方差越大,说明权重差别越小,因此表示不强调这一因素的影响,反之,则表示更强调这一因素导致的权重的不均衡。因此:
两个方面的某个的 sigma 相对变小 表示这一方面相对较重要,得到强调。如 sigma_d 变小,表示更多采用近邻的值作平滑,说明图像的空间信息更重要,即相近相似。如 sigma_r 变小,表示和自己同一类的条件变得苛刻,从而强调值域的相似性。
其次,sigma_d 表示的是空域的平滑,因此对于没有边缘的,变化慢的部分更适合;sigma_r 表示值域的差别,因此强调这一差别,即减小 sigma_r 可以突出边缘。
sigma_d 变大,图像每个区域的权重基本都源于值域滤波的权重,因此对于空间邻域信息不是很敏感;sigma_r 变大,则不太考虑值域,权重多来自于空间距离,因此近似于普通的高斯滤波,图像的保边性能下降。因此如果像更多的去除平滑区域的噪声,应该提高 sigma_d ,如果像保持边缘,则应该减小 sigma_r 。
极端情况,如果 sigma_d 无穷大,相当于值域滤波;sigma_r 无穷大,相当于空域高斯滤波。
最后,公式中的$||x||$表示向量的范数,
举例:
If $x = (x1, x2, x3)$ then $||x|| = (x1^2 + x2^2 + x3^2)^{0.5}$
代码实现
主要来自laurencebho/iproc: Bilateral filter & joint bilateral filter (github.com),就不再重复贴了,主要逻辑比较清晰,不过注释较少。更易懂的代码实现方式可以看这篇文章–实现图像的联合双边滤波处理_ALTLI的博客,其运行速度优化得也更好。